Cylinder Fun

One of the many oddball questions festering in the back of my skull for the last year had to do with finding the volume of a cylinder. The most common methods in calculus for determining the volume of such a solid make use of discs or shells; I've never found these very satisfying. The reason for this is I prefer to think about solids of revolution as being composed of infinitely many wedge-shaped slices of infinitesimal volume. This is far more intuitive to me than discs and shells, and the idea works for many other solids.

Taken from Make It With Me

Consider a simple cylinder of radius r and height h. These two lengths compose a square or rectangular slice from the center of the cylinder to its radius circumference* (or vice versa). This is effectively a pie-shaped wedge with arc length s approaching zero. The idea is readily expressed as the limit of a Riemann Sum.

In terms of r and θ, this is effectively an infinite number of pie-shaped wedges with angle θ approaching zero, whose volumes are composed of the area rh multiplied by the infinitesimal dθ.

Note the "1/2" included in each of these equations. Because I'm using pie wedges instead of the typical fare, the infinitesimals are slightly skewed. By themselves, they would merely extrude the area A(w_k) into a rectangular prism--definitely not what we want. Instead, we need to take the average of the arc lengths at both ends of the radius to create the appropriate infinitesimal: one end of the radius will move arc length rθ, the other end won't move at all. Thus we replace ∆θ with (r∆θ + 0)/2 or (1/2) r∆θ. Having done this, we now convert to integral notation:

And because we intend to find the volume of the whole cylinder, we replace the interval [a,b] with [0,2π] and rearrange to obtain:

Polar graph of r=√(2π/θ) from Wolfram Alpha

Taking a Limit

Another idea related to the cylinder has to do with forming a rectangle from sectors of a circle by taking the limit of their length when stacked in an alternating pattern, rather like this:

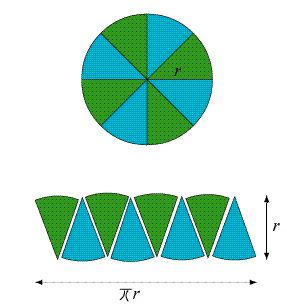Taken from the Victoria Department of Education

This is by no means an uncommon way to think about the area of a circle, but I had never before seen anyone actually obtain the limit--it was always verbally inferred.

The method I use to articulate this limit expresses the chord length of each sector, and the number of sectors, in terms of the central angle θ. As the angle becomes smaller and smaller, the arc lengths will effectively come to equal the chord lengths. For each sector's chord length, we have:

Notice that each side of the sector stack is composed of 1/2 the total number of sectors. Hence, the length of all the chords on a side will be equal to

where n is the total number of sectors. Expressing n in terms of θ and rearranging, we obtain:

Then take the limit.

Limit of y=(2π/x) taken from Wolfram Alpha

We now have a rectangle with sides πr and r, giving us an area πr² equal to the area of the circle. We can use this to either multiply by the height h or solve the following integral:

Either way, it completes an interesting exploration of some important concepts in calculus.


[Errata]
* Thanks to Don "The Mathman" Cohen for the correction. I was thinking in terms of a unit circle, referring to the point to which the radius extends merely as "the radius." However, "circumference" far more effectively conveys my intent.